선형회귀 (Linear Regression)
: 독립 변수 x값을 통해 종속 변수 y값을 설명하는 것
- 이 때 독립 변수가 1개라면 단순 선형 회귀라 하며, 2개 이상인 경우를 다중 선형 회귀라 함
--> 예시) y = ax + b (단순), y = ax + a'x' + a''x'' + ... + b (다중) - 선형 회귀에서의 딥러닝은 기울기와 절편을 정확히 예측하는 데 사용된다.
즉, 예측선을 정확하게 그림으로써 새로운 x(입력값)에 대하여 정확한 y(예측값)을 도출하는 목표를 두는 것이다
최소제곱법 (Method of least squares)
: 주어진 선형 방정식이 단순 선형 방정식인 경우, 최소 제곱법을 통해 기울기와 절편을 바로 구할 수 있음
- x값이 입력값이고, y값이 출력값인 y = a*x + b 인 단순 선형 방적식에서의 최소 제곱법
--> a(기울기) = (x - x의 평균) * (y - y의 평균)의 합 / (x - x의 평균) ^2 의 합
--> b(절편) = y의 평균 - (x의 평균 * 기울기)
평균 제곱 오차 (Mean Square Error, MSE)
: 각 입력 데이터들에 대해 그은 선과의 오차를 계산하여 오차률이 작은 선을 그을 수 있도록 해야한다. 이 때 선과의 오차률의 평균을 구하는 방법을 MSE라 한다
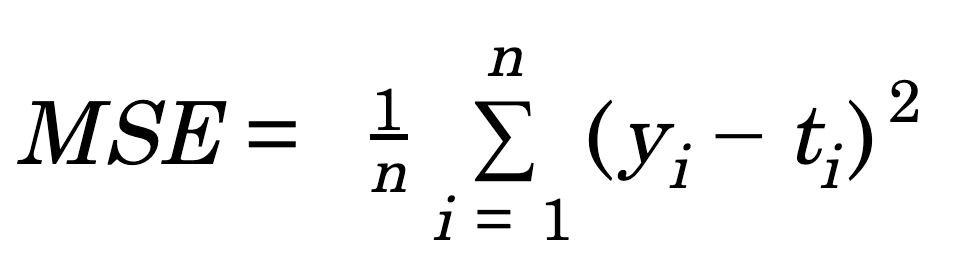
MSE 코드 작성해보기


'artificial intelligence' 카테고리의 다른 글
| 0710 HW (0) | 2021.07.13 |
|---|---|
| 0703 HW _ class summary (2) (0) | 2021.07.05 |
| 0703 class summary (1) (0) | 2021.07.05 |
| 0529 HW (0) | 2021.05.30 |


